트리 ( Tree )
트리란? 부모 자식 관계를 가진 자료구조이며 나무의 뿌리? 를 연상캐하는 자료구조입니다.

트리를 구성하는 요소로 노드와 간선으로 표현되어 구성되어있다.

위의 구성 노드를 구성한 코드입니다.
public class Node {
private int value;
private Node left;
private Node right;
}
데이터 표현은 int로 받기위해 int 타입으로 구성하고 왼쪽 오른쪽 노드를 구성하였습니다.
트리의 특징 및 구성요소
- 비선형 구조이며 계층구조를 나타낸다.
- 각 노드는 하나의 부모노드를 가진다.
- 자식 노드 개수는 0개 이상을 가진다.
- 노드 개수가 n일 때, 간선의 개수는 n-1개 이다.
이진트리 ( Binary Tree )
각각의 노드는 최대 2개의 자식 노드를 가질 수 있는 트리를 말합니다.

너비 우선 탐색 (Breadth-First Search) 구현
너비 우선 탐색이란 루트부터 시작하며 자식 노드를 왼쪽에서부터 오른쪽 순서대로 탐색하는 방법입니다.

큐를 사용하는 방법으로 구현하겠습니다.
- 동작원리
- 처음 시작점 루트 노드를 큐에 삽입
- 큐가 비어 있지 않을 때까지 반복문을 호출하고 큐에서 노드 하나를 꺼내온다.
- (1) 에서 저장한 노드값의 왼쪽 오른쪽 자식 노드가 존재하는지 확인한다.
- (2)에서 꺼낸 노드의 왼쪽 오른쪽 자식 노드를 순차적으로 큐에 저장한다.
- (3) (4) 의 순서를 반복한다.
- 큐가 비어있으면 반복문이 종료되고 너비 우선 탐색이 종료된다.
구현 코드
public void bfs(Node root) {
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
// 큐가 비어 있지 않을 때까지 반복
while (!queue.isEmpty()) {
Node node = queue.poll();
// 왼쪽 자식 노드가 있는지 확인
if (node.getLeft() != null) {
queue.offer(node.getLeft());
}
// 오른쪽 자식 노드가 있는지 확인
if (node.getRight() != null) {
queue.offer(node.getRight());
}
}
}
이진 탐색 트리 ( Binary Search Tree )
노드와 자식이 두 개 이하인 트리를 이진 트리라고 배웠다.
이진 트리를 활용하여 데이터 탐색을 용이하게 활요하도록 한 것이 이진 탐색 트리이다.
루트를 기준으로 루트보다 작은 값은 좌측으로 배치하고 큰 값은 우측으로 배치한다.
이진 탐색의 조건
- 유일한 값이여야 한다.
- 왼쪽 서브트리의 값< 루트 노드 값 < 오른쪽 서브트리의 값
- 자식이 2개 이하여야 한다.
재귀함수 사용
// 재귀
public Node search(Node root, int value) {
if (root == null) {
return null;
} else if (root.getValue() == value) {
return root;
} else if (root.getValue() > value) {
return search(root.getLeft(), value);
} else {
return search(root.getRight(), value);
}
}
반복문 사용
// 반복문
public Node search(Node node, int value) {
Node target = node;
if (target == null) {
return null;
}
while (target != null && target.getValue() != value) {
if (target.getValue() > value) {
target = target.getLeft();
} else {
target = target.getRight();
}
}
return target;
}
전위 순회
루트 노드부터 탐색하고 왼쪽 자식 노드에서 오른쪽 자식 노드를 탐색하는 순회 방법이다.
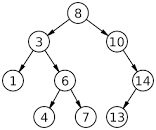
위의 트리 그림으로 전위 순회로 탐색하여 어떻게 탐색 되는지 알아봅시다.
- 루트 노드 8 부터 시작- > 8저장
- 8의 왼쪽 자식이 있는지 확인 → 어? 3이 있네? → 3 저장 → 3의 왼쪽 자식이 있나?
- 어? 1이 있네? 그럼 1을 저장 → 왼쪽 자식이 있나? 없네? → 기준 노드 3으로 올라가서
- 3의 오른쪽 자식 노드가 있나? 6이 있네? 6 저장
- 6의 왼쪽 자식이 있나? 4가 있네? 또 4 저장~ → 다시 6으로 올라가 오른쪽 자식이 있나 확인 → 7이 있네? 저장~
- 왼쪽 서브트리는 탐색이 다 되었다!
- 다시 루트 노드로 올라가자 → 8의 오른쪽 자식이 있나? 10 이 있네 ? 저장~
- 10의 왼쪽 트리가 있나? 없네? 오른쪽 트리가 있나? 14가 있네 저장
- 14의 왼쪽 노드가 있나? 13 있다 저장~ → 다시 14로 올라가 오른쪽 자식 노드가 있나? 없네, 순회 종료~
순서 : 8-3-1-6-4-7-10-14-13
코드 구현
public static void preOrder(TreeNode node, List<TreeNode> list) {
if (node == null) {
return;
}
list.add(node);
preOrder(node.getLeftChildren(), list);
preOrder(node.getRightChildren(), list);
}
중위 순회
전위 순회와 다르게 왼쪽 자식 노드부터 시작하여 기준 노드 그다음 오른쪽 자식 노드를 순회하는 방법입니다.

위의 그림으로 어떻게 순회되는지 확인 해 봅시다.
- 루트노드 8부터 시작하는데 왼쪽 자식노드가 있는지 확인하자 → 3이 있네? → 3의 왼쪽 자식 노드가 있나? → 1 이 있네? 1의 왼족 자식이 있나? 없네? 그럼 1 저장 →
- 기준 노드 3으로 올라가 → 3 저장 → 3의 오른쪽 자식 노드가 있는지? 6이 있네?
- 그럼 6의 왼쪽 자식 노드가 있나? 4가 있네 4 저장 → 다시 6으로 돌아가 6 저장 → 오른쪽 자식 노드가 있나? 7이 있네 저장~ → 7의 자식 노드가 있나? 없네 다시 6으로 올라가 → 그리고 3으로 올라가 → 다음 루트노드 8로 올라가 8 저장
- 왼쪽 서브 트리는 순회가 끝났다.
- 루트 노드 8의 오른쪽 자식 노드가 있나 ? 10 이 있네? 10 저장 → 10의 왼쪽 노드가 있나 → 오른쪽 노드는 있나? 14가 있네? 그럼 왼쪽 노드가 있나?
- 13이 있네 13 저장 → 14로 올라가 14 저장 하고 순회 종료
순서 : 1-3-4-6-7-8-10-13-14
코드 구현
public void inOrder(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
inOrder(node.getLeftChildren(), list);
list.add(node.getValue());
inOrder(node.getRightChildren(), list);
}
후위 순회
후위 순회는 루트노드를 마지막으로 탐색하고 왼쪽 자식 노드 방문 후 오른쪽 자식 노드 방문하고 기준 노드를 방문 하는 방법입니다.

위 그림으로 살펴봅시다.
- 루트 노드 8의 왼쪽 자식이 있나? 3이 있네 → 3의 왼쪽 자식이 있나? 1 있네 저장 → 3으로 올라가
- 3의 오른쪽 자식이 있나? 6 있네? → 6의 왼쪽 자식이 있나? 4 있네 4저장 → 다시 6으로 올라가 → 오른쪽 자식은? 7 있네 저장 → 6으로 올라가 6 저장 → 3으로 올라가 3 저장
- 루트 노드로 올라가 오른쪽 자식 노드가 있나? 10 있네
- 10의 왼쪽 노드가 있나? 없네 오른쪽 노드는? 14가 있네
- 14 노드의 왼쪽 노드는 ? 13있네 저장
- 14로 올라가 14 저장 → 10으로 올라가 10 저장
- 루트 노드 8로 올라가 8 저장
순서 : 1-4-7-6-3-13-14-10-8
코드 구현
public void postOrder(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
postOrder(node.getLeftChildren(), list);
postOrder(node.getRightChildren(), list);
list.add(node.getValue());
}
'Algorithms' 카테고리의 다른 글
| [Sort] 퀵 정렬 (Quick Sort) (0) | 2022.06.26 |
|---|---|
| [Sort] 병합 정렬 (Merge Sort) (0) | 2022.06.26 |
| [Sort] 셸 정렬 (Shell Sort) (0) | 2022.06.26 |
| [Sort] 삽입 정렬 ( Insertion Sort) (0) | 2022.06.26 |
| [Sort] 선택 정렬 (Selection Sort) (0) | 2022.06.26 |
| [Sort] 버블 정렬 (Bubble Sort) (0) | 2022.06.26 |
| [Sort] 선형 탐색 (Linear Search) (0) | 2022.06.26 |
| [JAVA] 해싱 동작 방식 (0) | 2022.01.17 |
![[Tree] 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FHmtP4%2FbtrGTxJDlGM%2FAAAAAAAAAAAAAAAAAAAAAHwHVJZurYdynbybrDqzEn98slQzSppZ_01eAth2fEud%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1767193199%26allow_ip%3D%26allow_referer%3D%26signature%3DT94eEzNruQyhiYlZ9Lvr0FhCopg%253D)